sheel
I love Asm
@Comfreek:
Zu bestimmten Funktionen hab ich schon Forenbeiträge gesehen,
wo das indirekt von WA-Mitrbeitern sogar bestätigt wurde.
Wenn ich sie nur wieder finden würde...
Stattdessen gibts drei konkrete Beispiele:
a)
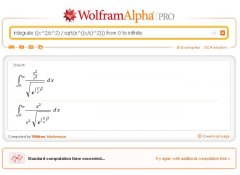
Bild 1, ein Integral, gelöst (und händisch die Korrektheit nachweisbar)
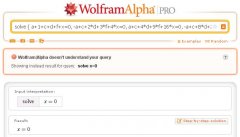
Bild 2, ist das Selbe.
(Falls es wer nicht weiß: a^(-b) <=> 1/(a^b)
und a^(b*c) <=> (a^b)^c
und a^0.5 <=> Quadratwurzel a
(wobei ^ nicht Xor, sondern Potenzieren ist))
Selber Ausdruck also.
WA gibt ziemlich damit an (oder hat es in der Vergangenheit zumindest),
den einzigen vollständigen automatischen Integrierer der Welt zu haben
(der mit wirklich jedem Ausdruck zurechtkommen soll).
Und die Umformung in den Reellen/komplexen Zahlen ist trivial
(und anderes Zeug sollte eigentlich ohne hinschreiben nicht rein kommen)
Ergebnis, wie man sieht: Es hat erkannt, dass Bruchnenner unter den Bruchstrich kommen,
und dann war die Rechenzeit aufgebraucht (noch dazu in der Bezahlversion, die so eine Beschränkung beim Bezahlen noch nicht hatte. Genau deswegen wurde eigentlich gezahlt)
b)
Ein lin. Gleichungssystem. Irgendwas wie
Bild drei zeigt, dass WA sowas lösen kann (im Bild sind zu wenig Gleichungen,
um eindeutige Werte zu bekommen, aber es wurde immerhin so weit wie möglich gemacht)
Gibt man mehr Gleichungen dazu (noch 3, damit wären eindeutige Zahlenlösungen möglich):
WA kanns plötzlich nicht mehr parsen.
Ich hätte Verständnis dafür, dass es heißt "Zu viel Arbeit ohne Gegenleistung".
Da das noch immer die Bezahlversion ist gilt das aber nicht.
Und dass es alles plötzlich nicht mehr parsen kann...
(und es ist kein Syntaxfehler drin. Jede der 5 Gleichungen einzeln wird verstanden,
Kombinationen von 2-4 Gleichungen auch, aber 5 zusammen ist zu viel...)
c)
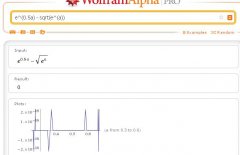
Bild 5
Ein Ausdruck minus den selben, nur anders hingeschrieben (teilweise wieder die Formeln von a).
x-x ist für mich 0, diesmal hat es die Umformung auch geschafft ("Result: 0").
Trotzdem sind im Diagramm darunter interessante Zacken...
Bei 10^(-16) denkt man an double-Rundungsfehler,
aber wenn der Input für die Diagrammerstellung das umgeformte "y=0" ist
ist sowas etwas unverständlich.
Und WA rechnet außerdem nicht mit normalen 32bit-Variablen
(2^90248 geht zu 100% genau auszurechnen,
aber manchmal gilt 0=10^(-16) eben einfach so...wtf)
Zu bestimmten Funktionen hab ich schon Forenbeiträge gesehen,
wo das indirekt von WA-Mitrbeitern sogar bestätigt wurde.
Wenn ich sie nur wieder finden würde...
Stattdessen gibts drei konkrete Beispiele:
a)
Bild 1, ein Integral, gelöst (und händisch die Korrektheit nachweisbar)
Bild 2, ist das Selbe.
(Falls es wer nicht weiß: a^(-b) <=> 1/(a^b)
und a^(b*c) <=> (a^b)^c
und a^0.5 <=> Quadratwurzel a
(wobei ^ nicht Xor, sondern Potenzieren ist))
Selber Ausdruck also.
WA gibt ziemlich damit an (oder hat es in der Vergangenheit zumindest),
den einzigen vollständigen automatischen Integrierer der Welt zu haben
(der mit wirklich jedem Ausdruck zurechtkommen soll).
Und die Umformung in den Reellen/komplexen Zahlen ist trivial
(und anderes Zeug sollte eigentlich ohne hinschreiben nicht rein kommen)
Ergebnis, wie man sieht: Es hat erkannt, dass Bruchnenner unter den Bruchstrich kommen,
und dann war die Rechenzeit aufgebraucht (noch dazu in der Bezahlversion, die so eine Beschränkung beim Bezahlen noch nicht hatte. Genau deswegen wurde eigentlich gezahlt)
b)
Ein lin. Gleichungssystem. Irgendwas wie
Code:
a+b+c=4
2a+3b+4c=-2
a+9b=10
Werte für a,b,c sind...?um eindeutige Werte zu bekommen, aber es wurde immerhin so weit wie möglich gemacht)
Gibt man mehr Gleichungen dazu (noch 3, damit wären eindeutige Zahlenlösungen möglich):
WA kanns plötzlich nicht mehr parsen.
Ich hätte Verständnis dafür, dass es heißt "Zu viel Arbeit ohne Gegenleistung".
Da das noch immer die Bezahlversion ist gilt das aber nicht.
Und dass es alles plötzlich nicht mehr parsen kann...
(und es ist kein Syntaxfehler drin. Jede der 5 Gleichungen einzeln wird verstanden,
Kombinationen von 2-4 Gleichungen auch, aber 5 zusammen ist zu viel...)
c)
Bild 5
Ein Ausdruck minus den selben, nur anders hingeschrieben (teilweise wieder die Formeln von a).
x-x ist für mich 0, diesmal hat es die Umformung auch geschafft ("Result: 0").
Trotzdem sind im Diagramm darunter interessante Zacken...
Bei 10^(-16) denkt man an double-Rundungsfehler,
aber wenn der Input für die Diagrammerstellung das umgeformte "y=0" ist
ist sowas etwas unverständlich.
Und WA rechnet außerdem nicht mit normalen 32bit-Variablen
(2^90248 geht zu 100% genau auszurechnen,
aber manchmal gilt 0=10^(-16) eben einfach so...wtf)