Figur mit oder gegen Uhrzeigersinn

[kuhlmaehn]

Super, danke. Jetzt hab ichs verstanden. Dann brauch ich ja gar nicht den Mittelpunkt =) (hab gerade verzweifelt gesucht wie ich den berechnen soll :X)
Dann werd ich das mal probieren in eine Funktion einzubauen

 

[kuhlmaehn]

So ich hab es jetzt endlich geschafft daraus einen Rechenvorgang zu machen, jedoch kommt bei meiner Rechung etwas positives heraus obwohl es nach rechts geht.
Ich hoffe aus der Grafik wird klar wo ich einen Fehler mache.

 

[Mamphil]

Hi,

das Problem ist, dass beim Cosinussatz die Orientierung verloren geht. Ich mach mir mal ein paar weitere Gedanken...

Mamphil

 

[Tobias Menzel]

... bekommst Du den Winkel nicht korrekt, wenn Du ihn mit dem Arkustangens berechnest und dann eine Quadrantenkorrektur (es ist ja bekannt, ob ein Punkt im kartesischen Koordinatensystem höher/tiefer bzw. links/rechts von einem anderen sitzt) durchführst?

Leider habe ich im Moment grade nicht viel Zeit, kann aber demnächst vielleicht auch mal herumprobieren.

Gruß
.

 

[Mamphil]

Hi,

bitte lies dir die Anlage durch (in Ermangelung eines Scanners abfotografiert)

Mamphil

edit:
Wichtig: Bitte meinen Nachtrag zwei Beiträge weiter beachten

 

[Mamphil]

Wichtig:
Meine oben vorgeschlagene Lösung ist absoluter Schwachsinn: Was passiert, wenn ein oder beide Vektoren unter e1 liegen?

Ich denk nochmal ;-)

Mamphil

 

[Mamphil]

Hi,

ich habe mir nochmal ein paar Gedanken gemacht:
Das in meinem Beitrag vorgeschlagene Verfahren ist IMHO doch nicht so verkehrt. Es ist nur eine kleine Modifikation notwendig:

Die Winkel Alpha 1 und 2 werden wie gehabt berechnet. Falls die y-Komponente des Vektors a bzw. b negativ ist, muss der berechnete Winkel noch mit -1 multipliziert werden.

Anschließend kann der Winkel zwischen a und b wie beschrieben berechnet werden.

Mamphil

 

[kuhlmaehn]

Puh, ein Glück geht es doch ich hab jetzt ne gute Stunde gebraucht das halbwegs zu verstehen ^^
Vielen Dank erstmal auf jeden Fall

Ich komm jedoch unten bei der "Aufpassen"-Stelle nicht weiter.
Ich hab jetzt mal Alpha1 und Alpha2 ausgerechnet:
Das müsste doch so richtig sein (oder?):
Alpha1 = arc cos [ 2*1 + 2*0 / Wurzel(2*2 + 2*2) ] = 45° //Skalarprodukt!?
Alpha2 = arc cos [ 2*1 + 0*0 / Wurzel(2*2+ 0*0) ] = 2 / 2 = 1 => arc sin von 1 = 0°

Also: Winkel zwischen a und b = alpha1 - alpha2 = 45°

Ich verstehe nicht was du da unten noch gemacht hast und warum ist das wieder nichts negatives?

 

[Mamphil]

Alpha2 = arc cos [ 2*1 + 0*0 / Wurzel(2*2+ 0*0) ] = 2 / 2 = 1 => arc sin von 1 = 0°

Da stimmt irgendetwas nicht ;-)

a (T) b, (T) hochgestelltes T: "a transponiert b", entspricht dem Skalarprodukt als Matrixmultiplikation ausgedrückt

"Aufpassen" bezog sich darauf, was die Funktion arccos liefert, ich glaube im Nachhinein aber nicht, dass es damit Probleme gibt...

Zum Thema "Negativ / Positiv": Bei meinem letzten Vorschlag ist "Linksabbiegen" negativ, "Rechtsabbiegen" positiv, also umgekehrt, als bei der ersten Idee.

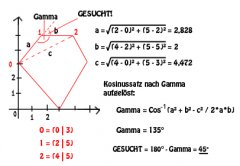
Schau dir mal das angehängte Beispiel an...

Mamphil

 

[kuhlmaehn]

Das klappt jetzt wirklich super, vielen Dank!

Ich hab mit meinem Programm jetzt mal probiert deine Bespiele nachrechnen zu lassen und das klappt auch super nur verstehe ich nicht beim 2. Beispiel was du am Ende mit -206,6° = +135,4 meinst? Da hab ich erstmal doch eine negative Orientierung, also links herum raus!?
Und ich hab noch eine Verständnisfrage.. warum "verschluckt" aTb / |a|*|b| die orientierung aber mit dem "hilfsvektor" (nennt man das so?) e1 kann man sie ausrechnen?
Und warum kannst du sowas? ^^ Ich hoffe doch du studierst Mathe!?