Matthias Reitinger
ɐɯıǝɹ
Ich kann es ja mal versuchen. Aber ich warne jetzt schon: das wird bestimmt länglich und etwas mathematisch-theoretisch…Könntest Du es mal erklärenMal so für Halbschlaue..
Ein lineares Programm bzw. eine lineare Optimierungsaufgabe ist eine Aufgabe der Form:
maximiere c_1 * x_1 + c_2 * x_2 + … + c_n * x_n
unter den Nebenbedingungen:
a_1_1 * x_1 + a_1_2 * x_2 + … + a_1_n * x_n <= b_1
a_2_1 * x_1 + a_2_2 * x_2 + … + a_2_n * x_n <= b_2
…
a_m_1 * x_1 + a_m_2 * x_2 + … + a_m_n * x_n <= b_m
Oder nicht ganz so abstrakt formuliert: man hat n Variablen x_1, …, x_n und eine Zielfunktion c_1 * x_1 + c_2 * x_2 + … + c_n * x_n. Man sucht nun eine Belegung der Variablen mit konkreten Werten, sodass die Zielfunktion einen möglichst großen Wert annimmt. Die Werte, die die Variablen annehmen dürfen, unterliegen dabei aber bestimmten linearen Einschränkungen (den Nebenbedingungen).
Das klassische Beispiel für ein lineares Programm ist die Produktionsaufgabe: die Variablen x_1, …, x_n stehen für die Menge der zu produzierenden Güter im kommenden Monat (z.B. gibt x_1 an, wieviele Nägel die Fabrik herstellen soll, x_2 wieviele Konservendosen, x_3 wieviele Ölfässer…). Die Zielfunktion beschreibt den zu erwartenden Gewinn (die c_1, …, c_n geben also an, wieviel Gewinn man bei Produktion und Verkauf eines Nagels (c_1), einer Konservendose (c_2), eines Ölfasses (c_3) etc. macht). In den Nebenbedingungen stecken dann Einschränkungen, wie bspw. das im kommenden Monat zur Verfügung stehende Rohmaterial, die verfügbaren Maschinen, Arbeitskräfte usw. Lässt man nun einen LP-Solver auf dieses Problem los, erhält man am Ende eine Variablenbelegung (also die Mengen der zu produzierenden Güter pro Typ), mit der die Produktionskapazitäten optimal (im Sinne von: den maximalen Gewinn erzielend) ausgenutzt werden.
Was hat das nun mit Punkten und Dreiecken zu tun?
Der wirklich knifflige Teil sind dann die Nebenbedingungen bzw.die Iteration: wie soll man die Variablen einschränken, damit man nur Dreiecke erhält? Ein erster Schritt wäre, zunächst einmal nur Polygone zu erzeugen (also zusammenhängende Kantenzüge, die zudem auch noch geschlossen sind). Dazu kann man die Beobachtung nutzen, dass jede Ecke eines Polygons zu genau zwei anderen Ecken verbunden ist. In unser lineares Programm übersetzt heißt das: für jeden Ecke (jeden Punkt) muss die Anzahl der zu dieser Ecke verbundenen Ecken genau zwei sein. Wann sind nun zwei Ecken i und j verbunden? Genau dann wenn die Variable x_i_j den Wert 1 annimmt. Für ein festes i muss also die Nebenbedingung
x_i_1 + x_i_2 + … + x_i_n = 2
gelten (für jede Ecke sind also genau zwei dazugehörige Kanten „aktiv“). Wenn wir das LP lösen, erhalten wir dann auch wie erwartet eine Menge von Polygonen (die sich auch nicht schneiden – sich schneidende Polygone widersprechen der Optimalität).
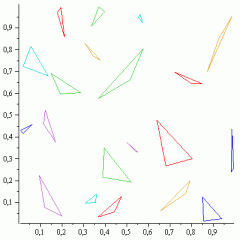
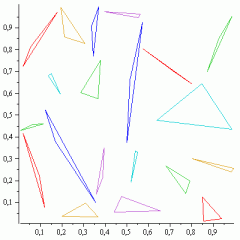
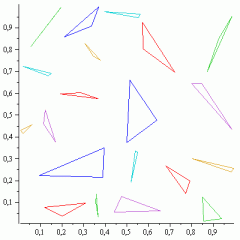
Ab da setzt dann die Iteration ein. Wir müssen die Lösung des LPs betrachten, also in diesem Fall die entstandenen Polygone. Wenn ausschließlich Dreiecke entstanden sind, dann sind wir bereits fertig. Andernfalls müssen wir zusätzliche Nebenbedingungen einführen, die bei der nächsten Iteration das Entstehen genau dieser Polygone (die keine Dreiecke sind) verhindert. Man fügt dem LP also zusätzliche Nebenbedingungen hinzu und lässt es wieder vom Solver lösen. Die Lösung testet man wieder auf Nicht-Dreiecke, fügt zusätzliche Nebenbedingungen hinzu um diese zu vermeiden, löst das erweiterte Problem wieder… usw. bis man bei einer Lösung angekommen ist, die nur Dreiecke enthält. Im Beispiel haben bereits 6 Iterationen ausgereicht, um die Lösung zu erhalten.
Jetzt könnte man sich natürlich fragen, warum man nicht einfach von vorneherein Nebenbedingungen hinzufügt, die das Entstehen von Polygonen mit mehr als drei Ecken verbieten bzw. das Entstehen von Dreiecken erzwingen. Dann müsste man das LP doch nur einmal lösen. Das Problem, in das man dabei rennt: man müsste dazu sehr sehr viele Nebenbedingungen hinzufügen. Das macht den Solver langsam (im schlimmsten Fall benötigt der Solver exponentielle Laufzeit in der Anzahl der Nebenbedingungen). Bei 6 Punkten mag es noch ganz gut funktionieren, bei 9 Punkten hat mein Rechner aber bereits über 10 Minuten für die Lösung benötigt. Bei allen 18 Punkten habe ich nach fast zwei Stunden abgebrochen. Vermutlich wäre die Lösung auch nach zwei Tagen noch nicht vorgelegen. Das iterative (man könnte auch sagen: adaptive) Verfahren nimmt dagegen nur einen Bruchteil dieser Nebenbedingungen mit auf und liefert trotzdem dasselbe Ergebnis. Abgesehen davon muss man das Problem in jeder Iteration nicht unbedingt komplett von Neuem lösen: der Simplex-Algorithmus – de facto der Standard-Ansatz zum Lösen linearer Programme – kann das bereits gefundene Optimum für einen „Warmstart“ beim Lösen des erweiterten linearen Programms verwenden. Der Nachteil, dass man den Solver mehrfach anschmeißen muss, verschwindet damit nahezu.
Ich hoffe das war jetzt ausführlich und verständlich genug. Wenn noch Fragen offen sind, nur zu
Und wo bekommt man solche Programmieraufgaben gestellt?Wofür ich den Algorithmus brauche?
Es ist eine Programmieraufgabe, die ich bekommen habe, gegebene Punkte zu Dreiecken zu verbinden, ohne dass sie sich überschneiden. Die Grundlagen habe ich schon alle (also das Programm, dass die Punkte aus der Datei liest und verarbeitet, ein Bild bereitstellt und die Punkte drauf markiert und auch Dreiecke zeichnen kann), nur mein Algorithmus will nicht.
Eine einfache und effiziente Möglichkeit wird es hier wohl nicht geben – wenn du darauf bestehst, dass die Umfangsumme minimal sein soll. Die Vermutung liegt nahe, dass es sich hierbei um ein NP-schweres Problem handelt. Wenn du diese Forderung fallen lässt und nur noch daran interessiert bist, die Punkte zu überschneidungsfreien Dreiecken zu verbinden, dann könnte die Sache anders aussehen.Es war einfach meine erste Idee, das mit den kürzesten Verbindungen zu machen, aber das scheint ja wohl nicht zu gehen. Daher suche ich jetzt eine bessere Möglichkeit.
Ein spontaner Einfall hierzu: Divide & Conquer. Finde eine Trenngerade, die die Punktemenge in zwei Punktemengen mit jeweils durch drei teilbarer Punkteanzahl trennt. Führe dies rekursiv durch, bis nur noch Punktemengen mit jeweils drei Punkten übrig sind, für die das Problem dann trivial ist. Gegebenenfalls Backtracking verwenden, falls man in eine Sackgasse läuft. Vorteil dieser Methode: leicht parallelisierbar. Nachteil: das Auffinden der Trenngerade könnte nicht ganz trivial sein… möglicherweise gibt es aber dazu schon passende Algorithmen.
Grüße, Matthias