Algorithmus zum Punkte verbinden

[multimolti]

@chmee:
Ja, du hast recht. Ich werde meine Fragestellung oben noch mal überarbeiten.

Noch mal eine Idee, wie ich Gumbos Vorschlag implementieren könnte:
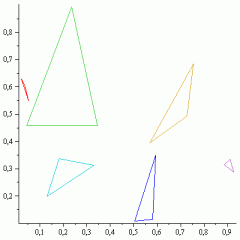
Ich rechne jede () verfügbare Möglichkeit durch, die Punkte irgendwie zu Dreiecken zu kombinieren, und rechne immer eine Gesamtlänge alles Linien aus. Dann nehme ich die mit der kürzesten Gesamtlänge.
Das würde die Vorraussetzung kurze Linien erfüllen, aber noch nicht das Problem mit dem Überschneiden der Linien. Und ich glaube, es würde recht lange brauchen, alle Kombinationen auszurechnen.

EDIT: @chmee:
"Du suchst einen Algorithmus der mehrere Dreiecke auf Deckung überprüft, und im vorliegenden Fall die Punkte neu gruppiert, oder ?"
Leider geht das nicht, ich habe festgelegte Punkte, die ich als Input-Daten bekomme. Was geändert werden kann ist die Kombination von 3 Punkten, die zu einem Dreieck verbunden werden, nicht jedoch die Punkte selbst.
Wie könnte ich denn prüfen, ob sich die Dreiecke überschneiden?

 

[Matthias Reitinger]

Noch mal eine Idee, wie ich Gumbos Vorschlag implementieren könnte:
Ich rechne jede () verfügbare Möglichkeit durch, die Punkte irgendwie zu Dreiecken zu kombinieren, und rechne immer eine Gesamtlänge alles Linien aus. […] Und ich glaube, es würde recht lange brauchen, alle Kombinationen auszurechnen.

Das glaube ich auch, da die Anzahl an möglichen Kombinationen mit der Anzahl der Punkte rapide ansteigt (bei 18 Punkten wie im Beispieldatensatz hab ich mir 190.590.400 Möglichkeiten errechnet, bin mir aber nicht ganz sicher ob das stimmt).

Wie könnte ich denn prüfen, ob sich die Dreiecke überschneiden?

Für einen groben Test reicht es zu prüfen, ob sich die Bounding Boxes (oder auch die Umkreise) der Dreiecke paarweise überlappen. Wenn dies für kein Paar von Dreiecken der Fall ist, gibt es schon mal sicher keine Überschneidungen zwischen den Dreiecken. Andernfalls muss man sich die Überlappungsfälle genauer anschauen, also einen „echten“ Dreieck-Dreieck-Schnitttest durchführen. Dazu kann man beispielsweise das „Separating Axes Theorem“ verwenden (einfach mal danach suchen, gibt einige Beschreibungen und Tutorials dazu).

Grüße, Matthias

 

[multimolti]

Okay, das klingt alles sehr gut, danke.
Wenn ich jetzt das „Separating Axes Theorem“ verwende, kann ich nur rausfinden, ob die Dreieckskombination die ich schon habe überlappt oder nicht. Aber am praktischsten wäre es doch, wenn mein Algorithmus gleich nur Dreiecke bilden würde, die sich nicht überlappen!

Hat jemand eine Idee, wie ich das realisieren kann? Sonst wird es sehr rechenaufwändig...

 

[Matthias Reitinger]

Aber am praktischsten wäre es doch, wenn mein Algorithmus gleich nur Dreiecke bilden würde, die sich nicht überlappen!

Dann müsstest du für jede neue Strecke, die du einziehen willst, testen, ob sie sich mit einem der bereits vorhandenen Dreiecke schneidet. Da eine Strecke auch nur eine konvexe Punktmenge ist, sollte sich das auch mit dem SAT lösen lassen. Möglicherweise ist hier aber der direkte Weg (Strecke-Strecke-Schnitttest) schneller, müsste man sich mal im Detail überlegen.

Hat jemand eine Idee, wie ich das realisieren kann? Sonst wird es sehr rechenaufwändig...

Da es sich wohl nicht vermeiden lässt, wiederholt die Schnitttests auszuwerten, wäre zu überlegen, ob man die Schnittinformationen nicht vorberechnet und dann auf eine entsprechende Lookup-Table zurückgreift (das hat chmee auch schon vorgeschlagen, wenn ich ihn richtig verstanden habe). Damit erhöht sich aber natürlich die Speicherkomplexität des Algorithmus.
Ansonsten hilft wohl nur ein „überlegtes“ Ausprobieren aller Möglichkeiten (d.h. frühes Ausschließen von Möglichkeiten, die sicher nicht zum Optimum führen etc., spezielle Heuristiken). Wenn du wirklich das Optimum (und nicht nur etwas, was nahe am Optimum liegt) herausfinden willst, könnte man das Problem auch als (ganzzahliges) lineares Programm formulieren und dann einen entsprechenden Löser darauf loslassen (Simplex-Algorithmus & Co.).
Darf ich abschließend noch die neugierige Frage stellen, wofür du einen solchen Algorithmus brauchst? Mir fällt da so spontan kein Anwendungsgebiet ein, darum würde mich interessieren, was der Hintergrund dazu ist.

Grüße, Matthias

 

[chmee]

Hab mir auch noch Gedanken gemacht..

Meine erste Idee ( Linienschnitte in Array aufführen ) schließt aber nicht aus, dass inneliegende Dreicke entstehen können..

Ja, das meinte ich mit Gruppierung in Tripel, vorgegebene Punkte zusammenführen zu geschlossenen Dreiecken.

Hmm, also vielleicht wäre erstmal ein Array aller möglichen Linien ein Anfang, die Größe des Array wäre Fakultät von n ( n! ). Darin könnte man schon mal die Punkte und die Länge jener Linie eintragen ( zB 1,2,12.2 ) und eine Kombination suchen, wo 1. nach Länge sortiert wird ( die Längsten sollen raus ) und 2. nach der Sortierung jeder Punkt in den ersten n/2 Ergebnissen nur jeweils 2x erscheinen darf. Tatsächlich ergibt sich das Dreieck schon, wenn zwei Linien einen Ausgangspunkt haben ( die anderen 2 Punkte ergeben die dritte Seite ). Logisch ist aber auch, dass nicht immer die kürzesten Linien die Überschneidung ausschließen.. Vielleicht wäre es auch sinnvoll, einen Logik-Baum zu erstellen. Möglicherweise ist auch das reine zufällige Durchtesten die schnellste Methode..

Sorry, ich schreibe einfach mal nur meine Gedanken auf, da müssen keine Ergebnisse dabei sein, zumindest Denkansätze.

Die andere Frage ist natürlich : Kann man mit jeder beliebigen 3*n fachen Wertesammlung auch 100%ig nicht überlappende Dreiecke erzeugen? Ist die Antwort NEIN, kann man nur alle Möglichkeiten durchgehen, um ein Ergebnis zu finden. Möglicherweise gibt es einen Algorithmus, um diese Frage zu beantowrten, zumindest hätte man dann recht schnell den Gegenbeweis..

mfg chmee

 

[Matthias Reitinger]

Hmm, also vielleicht wäre erstmal ein Array aller möglichen Linien ein Anfang, die Größe des Array wäre Fakultät von n ( n! ).

Ganz so schlimm ist es dann doch nicht. Es gibt n*(n-1)/2 mögliche Strecken, wenn mit n die Gesamtanzahl der Punkte gemeint ist.

Die andere Frage ist natürlich : Kann man mit jeder beliebigen 3*n fachen Wertesammlung auch 100%ig nicht überlappende Dreiecke erzeugen?

Nein. Trivialer Fall: die Punkte liegen alle im Ursprung. Oder sie liegen alle auf einer Geraden.

Grüße, Matthias

 

[chmee]

Ah, ich meinte nicht Fakultät, sondern Summe von n.

Ja, vielleicht darf man diese beiden Fälle ausschließen, alle Punkte auf einer Position und alle Punkt auf einer Geraden.

Ach ja, diese Links habe ich dazu noch gefunden:
http://public.tfh-berlin.de/~herrmann/entwicklungsprojekte/netzoptimierung/Netzoptimierung_K3_31.htm
http://elib.dlr.de/8626/

mfg chmee

 

[Matthias Reitinger]

Hallo,

ich hab mir mal den Spaß erlaubt und hab ein iteratives Lösungsverfahren basierend auf einem ILP-Solver implementiert. In weniger als einer halben Sekunde Laufzeit wurde so ein Optimum (bezüglich minimaler Summe der Seitenlängen) für den Beispieldatensatz errechnet (siehe Anhang). Das Interessante daran: über die Nebenbedingungen musste ich nur dafür sorgen, dass Dreiecke entstehen. Die Überlappungsfreiheit steckt implizit in der Optimalität (Minimalität) der Lösung mit drin (eine Lösung mit Überlappungen ist immer suboptimal – es sei denn natürlich es existiert keine Lösung ohne Überlappungen). Das bedeutet, dass man bei einem spezialisierten Algorithmus für dieses Problem auf die Überlappungen überhaupt nicht achten muss, sofern garantiert ist, dass das Optimum gefunden wird.

Grüße, Matthias

 

[chmee]

Könntest Du es mal erklären Mal so für Halbschlaue..

mfg chmee

 

[multimolti]

Wofür ich den Algorithmus brauche?

Es ist eine Programmieraufgabe, die ich bekommen habe, gegebene Punkte zu Dreiecken zu verbinden, ohne dass sie sich überschneiden. Die Grundlagen habe ich schon alle (also das Programm, dass die Punkte aus der Datei liest und verarbeitet, ein Bild bereitstellt und die Punkte drauf markiert und auch Dreiecke zeichnen kann), nur mein Algorithmus will nicht.
Es war einfach meine erste Idee, das mit den kürzesten Verbindungen zu machen, aber das scheint ja wohl nicht zu gehen. Daher suche ich jetzt eine bessere Möglichkeit.