✔ Algorithmus - Weg finden

[Vereth]

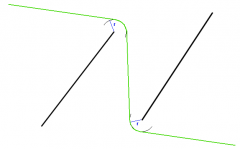
Sorry, ich war etwas voreilig. Mein Vorgehen hat den Fehler, dass das 'Tunneln' durch Eckpunkte von Streckenzügen nicht genügend berücksichtigt wird; du hattest auf das Problem schon hingewiesen, Matthias:-(.
Man kann das Problem aber vermeiden und trotzdem zu einer guten Näherung kommen. Man erstellt aus den Punkten, Start- und Zielpunkt ausgenommen, ein Voronoi-Diagramm; dadurch bekommt man Wegpunkte, die im freien Gebiet sind. Anschließend ergänzt man das Diagramm um Strecken, die zu Start- und Zielpunkt führen. Aus dem resultierenden Graphen entfernt man alle Kanten, die eine der vorgegebenen Strecken kreuzen. Dadurch erhält man einen planaren Graph, auf den man einen Algorithmus zur Wegsuche anwenden kann. Dies führt zumindest zu einer brauchbaren Näherungslösung.
Wenn einem das nicht reicht, kann man immer noch einen Algorithmus implementieren, der den Pfad verkürzt. Ich habe schon eine vage Idee, wie man so etwas machen könnte, aber es ist noch zu früh, darüber zu schreiben.

PS: Matthias, deine spontane Idee ist schon ein guter Ansatz, aber was geschieht, wenn du in einem Punkt ein ganzes Strahlenbündel hast?

 

[Matthias Reitinger]

Erst etwas off-topic:

PS: Ist das komplette Quoten eines unmittelbar vorhergehenden Beitrags nicht obsolet?

Darüber könnte man sich sicher vortrefflich streiten. Ich zitiere aus Prinzip die relevanten Teile, auf die ich mich beziehe. Ich weiß ja vor dem Abschicken meines Beitrages nicht, ob nicht inzwischen jemand anderer etwas geschrieben hat, wodurch dann nicht klar wäre, worauf ich mich beziehe. Grundsätzlich erst mal nicht zitieren und dann bei Bedarf nachträglich das Zitat reineditieren ist mir zu umständlich. Außerdem ist so auch immer klar, worauf ich mich beziehe, selbst wenn ein Beitrag außerhalb seines Kontexts auftritt.

PS: Matthias, deine spontane Idee ist schon ein guter Ansatz, aber was geschieht, wenn du in einem Punkt ein ganzes Strahlenbündel hast?

Der Fall kann nicht auftreten, denn sonst hätte der OP ihn schon erwähnt Nein, im Ernst, mein Verfahren macht natürlich Probleme, wenn mehr als zwei Strecken an einem Punkt enden.

Mir kommt gerade noch eine Idee, die aber nur in einem Spezialfall funktioniert: bilde zu jeder Gruppe zusammenhängender Strecken die konvexe Hülle der Punktmenge. Wenn sich die konvexen Hüllen nun nicht überschneiden und zusätzlich Start und Ziel in keiner der konvexen Hüllen liegen, dann kann man einfach die Eckpunkte der konvexen Hüllen als Knoten verwenden (+ Start und Ziel). Zwei Knoten sind genau dann durch eine Kante verbunden, wenn ihre direkte Verbindungslinie keine konvexe Hülle schneidet (oder die Punkte der gleichen konvexen Hülle angehören). Aber das ist dann schon eine wirklich spezielle Konstellation...

Das Problem, an das wir uns hier gerade annähern, nennt sich übrigens „Euclidean shortest path problem“. Im verlinkten Wikipedia-Artikel sind auch ein paar Paper aufgeführt, die vielversprechend klingen.

Grüße,
Matthias

 

[thomy800]

Man erstellt aus den Punkten, Start- und Zielpunkt ausgenommen, ein Voronoi-Diagramm; dadurch bekommt man Wegpunkte, die im freien Gebiet sind

So wie ich den Wiki-Artikel verstanden habe, werden bei dem Verfahren keine Punkte erstellt, sondern der Raum nur anhand von Punkten unterteilt. Wie stellst du dir das dann vor?

Ich glaube, das einzige Problem, was man lösen müsste, wäre, wie man die Kurven berechnet. Ich habe momentan eine Zwischenlösung: ich setze 3 Punkte um jeden Endpunkt einer Linie. Einer als Verlängerung der Linie, und 2 senkrecht dazu (links & rechts). Allerdings kürzt er das meist ab, heißt statt von links über mitte zu rechts wird gleich der mittlere Punkt gewählt (was ja logisch ist).
Optimal wäre daher ein Halbkreis um die Enden, wo der Weg so lange auf dem Kreis bleibt bis er sich wieder tangenziell entfernt.... nur wie setzt man das um?
(Zur Verdeutlichung noch mal ein Bildchen ^^)

 

[Vereth]

Die Idee mit der konvexen Hülle erscheint mir nicht sehr vielversprechend, weil u.U. zu viele Spezialfälle zu behandeln sind. Möglicherweise kann man sie aber eventuell bei der Optimierung eines gefundenen Weges wieder aufgreifen.
Ein Voronoi-Diagramm ist der duale Graph zu einer Delauny-Triangulation. Man trianguliert also zunächst den Raum (es muss nicht nach Delauny geschehen) und kann daraus dann den dualen Graphen ermitteln. Dadurch erhält man Punkte im freien Raum, die dann als Wegpunkte dienen können. Die Wege verlaufen dann entlang der Kanten des berechneten Quasi-Voronoi-Diagramms. Interessant könnte übrigens die Tatsache sein, dass jeder Knoten maximal drei Kanten hat (also vom Grad 3 oder kleiner ist) und der Graph planar ist, denn dadurch sind Schleifenbildungen unmöglich und die Anzahl der zu betrachtenden Wege bleibt überschaubar. Bevor man allerdings mit der Wegsuche beginnt, muss man erst diejenigen Kanten entfernen, die eine vorgegebene Strecke kreuzen.
Eine andere Vorgehensweise könnte sein, dass man als erstes irgendeinen Pfad sucht und diesen dann irgendwie optimiert. Die Suche könnte dann z.B. mit dem Pledge-Algorithmus durchgeführt werden. Allerdings muss man dabei einen Weg finden, Rundungsfehler bei den Winkelberechnungen zu vermeiden.

 

[thomy800]

Achso, so langsam versteh ich was du meinst ^^
Aber bei deinen Methoden ist nicht gewährleistet, dass es auch wirklich der kürzeste Weg ist, oder?
Im Prinzip soll ja das Resultat so aussehen, als hätte man eine Leine (mit dem Radius r) von A nach B (um die Hindernisse herum) gespannt. Nun könnte man die "Leine" auf unterschiedliche Wege spannen, aber das Problem habe ich nun schon mit A-Stern bewältigt bekommen, indem immer die kürzeste Strecke gewählt wird.

Ich habe mir auch überlegt, dass man theoretisch die Linien (Hindernisse) in ein Feld eintragen kann mit einer Dicke vom Radius r (von der Leine!). Dann kann man jeden einzelnen Pixel abklappern und mit A-Stern (oder womit auch immer) den Weg berechnen. Das Resultat sollte der gespannten Leine entsprechen (hat ja immer den Radius r als Abstand zu den Hindernissen). Das Problem: bei einer bestimmten Feldgröße dauert es auch entsprechend lange das Feld zu durchsuchen. Außerdem hätte ich das Ergebnis lieber in vektorieller Form...

Hat denn keiner eine Idee zu der Halbkreis-Geschichte?

 

[Vereth]

Das Problem bei deiner Methodik ist, dass du sicherstellen musst, dass dein 'mittlerer' Hilfspunkt nicht hinter einer zweiten Hindernisstrecke ist, weil er sonst als Zwischenpunkt einer Wegstrecke verwendet werden könnte, die diese kreuzt. Das kann geschehen, wenn die Endpunkte zweier Hindernisstrecken nahe genug beieinander liegen. Außerdem ist das Problem des Tunnelns durch einen Zwischenspunkt eines Streckenzuges noch ungelöst.
Bei meiner Methode können beide Fälle nicht auftreten. Als zusätzliche Hilfspunkte kann man auf der Mitte der triangulierenden Hilfsstrecken zusätzliche Punkte verwenden, um sicherzustellen, dass solche schmalen Durchgänge auch genutzt werden. Dadurch wird eine gute Annäherung an den optimalen Weg berechnet. Wenn man dann diese Näherung, beispielsweise mit einer Gummiband-Methode, glättet bzw. begradigt, bekommt man den tatsächlich optimalen Weg. Dabei wird allerdings vorausgesetzt, dass die Weglinie keine Dicke hat. Wenn das aber gefordert ist, muss der Algorithmus noch modifiziert werden.

 

[thomy800]

Das Problem bei deiner Methodik ist, dass du sicherstellen musst, dass dein 'mittlerer' Hilfspunkt nicht hinter einer zweiten Hindernisstrecke ist, weil er sonst als Zwischenpunkt einer Wegstrecke verwendet werden könnte, die diese kreuzt. Das kann geschehen, wenn die Endpunkte zweier Hindernisstrecken nahe genug beieinander liegen.

Ist das so ein Problem? Sowas kann man doch einfach checken. Muss man nur einmalig pro erstellten Punkt checken, ob der Radius auch zu den anderen Linien >= r ist.

Außerdem ist das Problem des Tunnelns durch einen Zwischenspunkt eines Streckenzuges noch ungelöst.

Damit meinst du die Kurven?

Bei meiner Methode können beide Fälle nicht auftreten. Als zusätzliche Hilfspunkte kann man auf der Mitte der triangulierenden Hilfsstrecken zusätzliche Punkte verwenden, um sicherzustellen, dass solche schmalen Durchgänge auch genutzt werden.

Ich schätze, der Aufwand solche schmalen Durchgänge zu finden und zu managen ist mindestens so hoch wie das Verfahren mit dem Abstand der anderen Linien.

 

[Vereth]

Ist das so ein Problem? Sowas kann man doch einfach checken. Muss man nur einmalig pro erstellten Punkt checken, ob der Radius auch zu den anderen Linien >= r ist.

Das ist aber nicht sehr effizient. Wenn du das für jeden Punkt deiner N Punkte machen willst, ist die Rechenzeit proportional zu O(N²). Zudem befürchte ich, dass durch deine zusätzlichen Punkte die Gefar besteht, dass dein Weg in eine ungünstige Richtung abgelenkt würde.

Damit meinst du die Kurven?

Ich glaube ja. Du hattest das Problem ja schon in einem deiner vorigen Posts angesprochen (genauer gesagt: diesem hier); dort hast du von Kurven gesprochen. Kurven sind aber gebogene Linien; wenn man gerade Linien hat, nennt man das Streckenzug. Aber ein solcher Punkt könnte auch Endpunkt mehrerer Strecken sein und nicht nur zweier. Und das meinte ich als ich oben von einem Strahlenbündel sprach.

Ich schätze, der Aufwand solche schmalen Durchgänge zu finden und zu managen ist mindestens so hoch wie das Verfahren mit dem Abstand der anderen Linien.

Das glaube ich nicht. Solche schmalen Durchgänge würden bei geschicktem Triangulieren automatisch mit einer Hilfskante versehen. Der Zeitaufwand z.B. für eine Delaunay-Triangulierung ist nur von der Größenordnung O(N*log(N)). Die in meinem vorigen Post erwähnten Hilfspunkte braucht man übrigens nicht, weil die Verbindungslinien zweier benachbarter Punkte eines Voronoi-Diagramms die Mittelsenkrechten der Triangulationskanten sind. Mein Vorschlag ist also:

1. Triangulierung, Zeitbedarf O(N*log(N))
2. Ermitteln aller M Schnittpunkte mit vorgegebenen Strecken, Zeitbedarf insgesamt O((N+M)*log(N))
3. (optional?)) Verfeinerung der Triangulierung an den Schnittpunkten, Zeitbedarf O(M) (grobe Schätzung von mir, möglicherweise auch etwas mehr)
4. Erstellen des Voronoi-Graphen, Zeitbedarf ?
5. Wegsuche, Zeitbedarf ca. proportional zu O(N'*log(N')+N'), N'=2*N
6. (nur, wenn Optimum verlangt ist) Kurvenglättung, Zeitbedarf ?

Bei Punkt 2 ist zu überlegen, ob dies nicht durch einen geeigneten Triangulierungs-Algorithmus vermieden werden kann. Punkt 3 entfiele dann auch.
Um für Punkt 6 den Zeitbedarf abschätzen zu können, müsste man erst einmal überlegen, wie ein solcher Algorithmus genau arbeiten soll. Momentan habe ich mir dazu noch keine großen Gedanken gemacht, aber vielleicht bekomme ich hier ein paar Anregungen. Vielleicht hat aber auch jemand anderes die passende Idee.
Hinweis: Der Zeitbedarf für 5 beruht auf der Wiki-Formel für den Dijkstra-Algorithmus. Die dort verwendeten Größen wurden von mir auf der Grundlage der Formeln für Dreiecksgraphen auf N reduziert, was zur obigen Formel führte.