✔ Algorithmus - Weg finden

[Thomas Darimont]

Hallo,

poste doch mal bitte ein paar Beispieldaten, mit dem man etwas herumspielen kann...

Gruß Tom

 

[thomy800]

@ SilentWarrior:
Ich glaube daraus lässt sich was machen
Man kann zusätzlich zu den Linien beim Generieren Rechtecke erstellen, wo die Linie die Mittellinie bildet. Die Rechtecke können dann die Breite 1 (2 Kanten) bekommen und die Länge der Linie (die anderen 2 Kanten).
An den 4 ecken kommen jeweils Knoten im Abstand r (vorrausgesetzt, sie liegen nicht in oder zu dich an einer anderen Wand). So ist gewehrleistet, dass ein Objekt zwischen den Lücken auch durch passt.

@ Thomas Darimont:
An was für Daten denkst du da? Ein Bildchen hatte ich ja schon erstellt (wo dementprechend Bsp-Daten eingetragen sind).

 

[Thomas Darimont]

Hallo,

@ Thomas Darimont:
An was für Daten denkst du da? Ein Bildchen hatte ich ja schon erstellt (wo dementprechend Bsp-Daten eingetragen sind).

Ich meine ein konkretes Beispiel mit Daten zu deinem Szenario:

Meine Umgebung (2D) besteht
a) aus Vektoren in einer Liste. Dies sind Linien mit einem Anfang und einem Ende, die bunt auf dem Feld verteild sind.
b) zusätzlich habe ich ein n*m-Feld aus boolischen Werten, wo diese Linien eingetragen sind.

Das Bild hilft dein Problem zu beschreiben... aber ohne sich erst selber Beispieldaten zu machen kann man dein Problem nur theoretisch bearbeiten...
Du könntest dir ja ein sinnvolles Datenformat ausdenken und dein Beispiel darin beschreiben. Dann kann man mit diesen Beispieldaten rumspielen.

Gruß Tom

 

[thomy800]

Etwas in der Art?

Radius r (Abstand) = 1
Linien: 2 (Vektorform)
Weg: hier nur einer, auch in Vektorform
Start (0|0) und Ende (7|6) sind eingetragen.

 

[Thomas Darimont]

Hallo,

ich dachte da eher an ein textformat (ähnlich wie wir es auch bei unseren coding quizes machen) das man leicht im programm einlesen kann.
Will man jetzt Beispiel nachmachen muss man die Linien / Punktkoordinaten erst noch aus dem Bild rausfummeln... den Schritt könntest du uns ersparen

Gruß Tom

 

[Matthias Reitinger]

Ich würde einfach für jede Mauer zwei Kanten und entsprechend vier Knoten machen. Die beiden Endknoten werden verbunden, wenn keine andere Mauer anliegt (und somit der Weg zur anderen Seite der Mauer nicht versperrt ist.

Ganz so einfach ist es leider nicht. Man muss jedem solchen Endknoten auch noch eine „Seite“ zuweisen und dafür sorgen, dass nur Knoten auf derselben „Seite“ mit diesem verbunden werden können.

Eine spontane Idee hierzu, die man erst noch verifizieren müsste:

• Betrachte den Eckpunkt Q der beiden Strecken PQ und QR.
• Erzeuge zu diesem Eckpunkt zwei Knoten. Nenne den einen Knoten „Innenknoten“ und den anderen „Außenknoten“.
• Vom Innenknoten aus dürfen nur Kanten zu anderen Knoten laufen, wenn deren zugehöriger Punkt S innen liegt, d.h.
  • S liegt bezüglich PQ in derselben Halbebene wie R und
  • S liegt bezüglich QR in derselben Halbebene wie P
• Vom Außenknoten aus dürfen nur Kanten zu anderen Knoten laufen, wenn deren zugehöriger Punkt S nicht innen liegt.

Grüße,
Matthias

 

[thomy800]

So, ich habe das Programm endlich hin bekommen. Allerdings, wie man an dem Resultat sieht, gibts da noch einen Haken.
Das Programm erstellt aus den Linien Rechtecke und an deren Ecken Punkte, die als Pfad verwendet werden können. Das Problem dabei ist, er verwendet nur welche, die da sind, und erstellt sich nicht neue, die den Weg evtl verkürzen würden.
Im ersten Bild ist der lange Pfad und im zweiten habe ich eine Linie hinzugefügt, die einen Punkt erstellt hat, der den Weg verkürzt, den das Programm selbstständig finden sollte...

edit: es könnte vielleicht aber auch an der Rechteck-Punkt-Verteilung liegen...

 

[Vereth]

Dein Problem, den kürzesten Pfad zu finden, ist eigentlich ganz einfach zu lösen.

1. Erweitere deine Streckenmenge mit Hilfe einer Delauny-Triangulation zu einem Netz
2. Finde in diesem Netz den kürzesten Weg

Fertig!

 

[Matthias Reitinger]

Dein Problem, den kürzesten Pfad zu finden, ist eigentlich ganz einfach zu lösen.

1. Erweitere deine Streckenmenge mit Hilfe einer Delauny-Triangulation zu einem Netz
2. Finde in diesem Netz den kürzesten Weg

Fertig!

Das ist gleich doppelt falsch:

1. Die Delauny-Triangulation enthält im Allgemeinen nicht den kürzesten Pfad.
2. Selbst wenn dem so wäre, hätte man immer noch das Problem, dass man bei Streckenzügen durch die Eckpunkte laufen könnte.

Grüße,
Matthias

 

[Vereth]

Verzeihung, ich habe vergessen

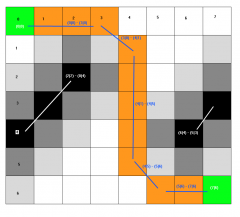
3. Verkürze den Weg, indem du Zwischenpunkte eliminierst, beispielsweise durch sukzessives Edge-Flipping.

Ob du dadurch wirklich immer das Optimum erreichst, hängt stark von dem Algorithmus ab, der beim Edge-Flipping verwendet wird, aber selbst bei einfachen Vorgehensweisen erreicht man dadurch relativ gute Ergebnisse, was, wie ich denke, für tomy800, wenn ich ihn richtig verstanden habe, auch akzeptabel ist, weil er zuerst geäußert hat, dass er froh wäre, wenn er überhaupt einen Weg finden könnte, was mit meiner Methodik ziemlich effizient zu implementieren ist. Puuuuuuuuuh

Matthias, bei Punkt 2 deiner Argumentation weiß ich nicht genau was du meinst. Sind Eckpunkte für dich die Eckpunkte des umschließenden Bereichs? Die muss man bei der Triangulation nur dann einbeziehen, wenn sie Endpunkte einer Strecke sind. Oder ist deine Befürchtung, dass der ermittelte Weg Endpunkte von Strecken beinhaltet, die nur Umwege verursachen? Diese Gefahr kann, wie in Punkt 3 angedeutet, minimiert werden.

PS: Ist das komplette Quoten eines unmittelbar vorhergehenden Beitrags nicht obsolet?