voll und vollständige Bäume

[reweiss]

Hi @ all,

ich hoffe ich bin hier richtig und ihr könnt mir helfen.

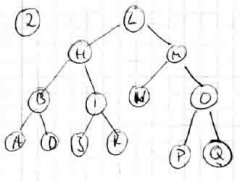
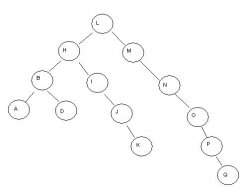
Gibt es irgendwie einen Weg wie ich einen vorhandenen binär Baum in einen vollen und in einen vollständigen binär Baum überführen kann? Ich kenne von AVL Bäumen diese Rotationsverfahren, aber kann ich die einfachen anwenden? Ich will den Baum ja nicht ausbalanzieren, ich will in ja nur in eine andere Darstellung bringen
Ich brauche keine Code dafür Ich will nur wissen wie ich das grafisch (also auf Papier zeichen) machen müsste!

Besten Dank schon mal....

 

[deepthroat]

Hi.

Ein Binärbaum muss eine ungerade Anzahl von Knoten haben damit du ihn in einen vollen Baum transformieren kannst.

Ein Binärbaum muss 2^(n+1)-1 Knoten (für n >= 0) haben damit du ihn in einen vollständigen Baum transformieren kannst.

Die Transformation könntest du so anstellen, das du von oben nach unten eine Ebene nach der anderen durchgehst und wenn irgendwo ein bzw. zwei Knoten fehlt/fehlen mußt du diesen durch Knoten von der darunterliegenden Ebene auffüllen.

Gruß

 

[reweiss]

Also hier mal der Baum den soll ich in einen vollen und in einen vollständigen Baum umwandeln. Wie würde der denn dann aussehen?

 

[Supa]

hy...

der Baum auf deiner Zeichnung ist soweit ich weiß aber kein korrekter Binär-Baum, oder?

muss nicht vom Knoten nach links weg immer nen kleiner wertiger Buchstabe stehn und nach rechts weg immer ein größerwertiger?

(siehe Anhang)

 

[deepthroat]

Hi,

hy...

der Baum auf deiner Zeichnung ist soweit ich weiß aber kein korrekter Binär-Baum, oder?

muss nicht vom Knoten nach links weg immer nen kleiner wertiger Buchstabe stehn und nach rechts weg immer ein größerwertiger?

(siehe Anhang)

Ein Binärbaum ist ein Graph mit einer Wurzel wo jeder Knoten bis zu 2 Kindknoten besitzt. Da spielt die Ordnung der Knoten überhaupt keine Rolle. Man kann natürlich Binärbaume zum sortieren einsetzen, z.B. als Heap.

@reweiss: Dein Baum ist bereits voll. Um den Baum vollständig zu machen müsstest du am Knoten N noch 2 Kindknoten dranhängen oder die Blätter A, D, J, K, P, Q entfernen; sonst geht das nicht.

Gruß