Polygonverschmelzung

genodeftest · 20. Juni 2012

…Naja, aber nicht allen. Stringkonkatenation ist quälend langsam implementiert in Java. Genauso BigInteger/BigDecimal. Und je nach JVM und Prozessor auch sämtliche trigonometrischen Funktionen mit double/float (wegen strictfp).

Thomas Darimont · 20. Juni 2012

Hallo,

…Naja, aber nicht allen. Stringkonkatenation ist quälend langsam implementiert in Java.
Genauso BigInteger/BigDecimal. Und je nach JVM und Prozessor auch sämtliche trigonometrischen Funktionen mit double/float (wegen strictfp).

...das mag für "aktuelle" / alte JVMs / JDKs ja sein... aber das ist ja nur ein Implementierungsdetail und eine Frage der Zeit (und Relevanz) bis sich "jemand" von offizieller Seite dem Problem annimmt- so kann das in einer neueren Version schon wieder ganz anders aussehen

Das gilt sowohl für Standard-Algorithmen / Verfahren im JDK als auch für die technischen Innereien der JVM wie z.Bsp. der Garbage Collector oder der JIT Compiler.

Bisher wurde die JVM mit jeder neuen (major) Version (IMHO) schneller - also verlasse ich mich hier im Normalfall darauf, dass die JDK / JVM Ingenieure schon dafür sorgen, dass die Performance der Implementierung auf hohem Niveau bleibt.

Wenn eine JVM / JDK Implementierung für eine konkrete Problemstellung nicht schnell genug ist, kann man dann bei wirklich performance-kritischem Code auf entsprechende Workarounds ausweichen. Diese können dann u.a. native Bibliotheken (vorsicht JNI overhead!) und / oder problemspezifischere Bibliotheken, Algorithmen und Datenstrukturen oder auch einfach eine Veränderung der Problemstellung sein

Btw. "schnelle" float sin/cos Implementierungen kann man auch in Java haben:
http://www.java-gaming.org/index.php?topic=24191.0

Ein Grund für Performance-Probleme bei der Verwendung von BigDecimal / BigInteger ist oft, dass diese Number Implementierung keine "spezielle" Unterstützung von Seiten der JVM erhalten - bzw. nicht so, wie es beispielsweise primitive Datentypen erfahren. -> Könnte sich ja mit der Zeit ändern ;-) Btw. je nach Anwendungsfall (z.Bsp. Multiplikation von großen Zahlen schafft die BigInteger Implementierung von https://github.com/tbuktu/bigint hier abhilfe

Ansonsten kann bei String-Performance Problemen die Implementierung der Klasse Text aus dem Javolution-Projekt (natürlich auch wieder je nach Anwendungsfall) Abhilfe schaffen (http://javolution.org/) ansonsten gäbe es hier auch noch Ropes: http://ahmadsoft.org/ropes/

Gruß Tom

genodeftest · 20. Juni 2012

Bisher wurde die JVM mit jeder neuen (major) Version (IMHO) schneller - also verlasse ich mich hier im Normalfall darauf, dass die JDK / JVM Ingenieure schon dafür sorgen, dass die Performance der Implementierung auf hohem Niveau bleibt.

Ja, sehe ich genau so.

Zu den Strings: Oder man nutzt StringBuilder/StringBuffer/…, die sind zumindest deutlich zügiger als der '+'-Operator. Aber das ist halt nicht die triviale Lösung.

Thomas Darimont · 20. Juni 2012

Hallo,

...
Es MÜSSEN auch nicht unbedingt beliebige Polygone sein, es reichen im NOTFALL (falls jemand dafür ne Lösung kennt) 6-Ecke..

Willst du wissen wann ein Objekt auf einer Landkarte / Landschaftsstruktur einen bestimmten "Karten"-Abschnitt betritt?

ist das ungefähr was du suchst? (Glaube nicht, da die Schnittpunkte wahrscheinlich nicht die sind, die du suchst - kannst du da vielleicht noch ein Beispiel machen?)

Ich denke das man das Problem auch gut parallelisieren und dann mit mehreren Prozessoren gleichzeitig lösen kann - wenn man die zu verarbeitende Datenmenge entsprechend aufsplittet. Man könnte beispielsweise die Polygone in sowas wie einem BSP-Tree ( http://en.wikipedia.org/wiki/Binary_space_partitioning) ablegen und aus diesem dann einzelne "Zellen / Spaces" parallel verarbeiten.

Ansonsten hört sich das nun für mich so an, als ob das hier ein Fall für GPGPU sein könnte

(wenns wirklich sau schnell sein soll)(http://de.wikipedia.org/wiki/General_Purpose_Computation_on_Graphics_Processing_Unit
http://cg-dev.ltas.ulg.ac.be/inf/Paper_46.pdf
)

Ansonsten die klassische Frage bei Performance.... wie schnell soll es denn sein? Was ist denn hier die Zielumgebung? Soll das tatsächlich "live" angezeigt werden? Sind die Polygone in Bewegung? Oder ist wird das "nur" für eine server-seitige Berechnung benötigt ohne direkte Anzeige?

Java:

package de.tutorials;

import java.awt.Color;
import java.awt.Graphics2D;
import java.awt.Polygon;
import java.awt.geom.Area;
import java.awt.geom.Line2D;
import java.awt.geom.PathIterator;
import java.awt.geom.Point2D;
import java.awt.image.BufferedImage;
import java.io.File;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

import javax.imageio.ImageIO;

public class UnionPolygonsExample {

	public static void main(String[] args) throws Exception {
		
		BufferedImage img = new BufferedImage(200, 200,BufferedImage.TYPE_INT_RGB);
		Graphics2D g = (Graphics2D) img.getGraphics();

		//Hexagone generieren
		Polygon p1 = generatePoly(100, 100, 40, 6);
		Polygon p2 = generatePoly(120, 120, 40, 6);
		
		// 2 Hexagone zeichnen
		Area a1_union = new Area(p1);
		Area a2_union = new Area(p2);
		a1_union.add(a2_union);
		g.setColor(Color.RED);
		g.draw(a1_union);  //Vereinigung zeichnen
		//g.fill(a1);

		Area a1_intersection = new Area(p1);
		Area a2_intersection = new Area(p2);
		a1_intersection.intersect(a2_intersection);
		g.setColor(Color.BLUE);
		//g.fill(a1_intersection); //Intersection zeichnen
		g.draw(a1_intersection);
		

		//Linien der Vereingungsmenge aufsammeln
		PathIterator pathItr = a1_intersection.getPathIterator(null);
		System.out.println(pathItr.getWindingRule());

		double[] current = new double[2];
		double[] first = null;
		double[] previous = null;
		List<Line2D> lines = new ArrayList<Line2D>();
		while (!pathItr.isDone()) {
			int coordType = pathItr.currentSegment(current);
			System.out.println(coordType + " -> " + Arrays.toString(current));
			if (previous != null) {
				lines.add(new Line2D.Double(current[0], current[1],previous[0], previous[1]));
			}else{ //this is the first iteration
				first = current.clone();
			}
			if(coordType == PathIterator.SEG_CLOSE){ //this is the last iteration
				lines.add(new Line2D.Double(current[0], current[1],first[0], first[1]));
			}
			previous = current.clone();
			pathItr.next();
		}
		
		// Schnittpunkte der Geraden ermitteln
		List<Point2D> intersectionPoints = new ArrayList<Point2D>();
		for (int i = 0, len = lines.size(); i < len; i++) {
			for (int j = i + 1; j < len; j++) {
				Line2D firstLine = lines.get(i);
				Line2D secondLine = lines.get(j);
				Point2D.Double point = computeIntersectionPoint(firstLine, secondLine);
				if(point != null){
					intersectionPoints.add(point);
					System.out.printf("Found intersection at: %s%n", point);
				}				
			}
		}

		//Schnittpunkte mit den geraden Zeichnen:
		g.setColor(Color.YELLOW);
		int r = 5;
		for(Point2D point : intersectionPoints){
			int x = (int)(point.getX()-r/2.0);
			int y = (int)(point.getY()-r/2.0);
			g.fillOval(x,y,r,r);
		}

		//Bildausgeben
		ImageIO.write(img, "png", new File("c:/polygonUnion.png"));
	}

	public static Polygon generatePoly(int x, int y, int r, int n) {
		//Quelle: http://www.informatik.htw-dresden.de/~iwe/grundlagen/java/galileo/java_140006.htm#Rxxjava_140006282NEckezeichnen
		Polygon p = new Polygon();

		for (int i = 0; i < n; i++)
			p.addPoint((int) (x + r * Math.cos(i * 2 * Math.PI / n)),
					(int) (y + r * Math.sin(i * 2 * Math.PI / n)));

		return p;
	}

	private static Point2D.Double computeIntersectionPoint(Line2D firstLine,
			Line2D secondLine) {

		float firstX1 = (float) firstLine.getX1();
		float firstX2 = (float) firstLine.getX2();

		float firstY1 = (float) firstLine.getY1();
		float firstY2 = (float) firstLine.getY2();

		float secondX1 = (float) secondLine.getX1();
		float secondX2 = (float) secondLine.getX2();

		float secondY1 = (float) secondLine.getY1();
		float secondY2 = (float) secondLine.getY2();

		float den = ((firstX2 - firstX1) * (secondY2 - secondY1))
				- ((firstY2 - firstY1) * (secondX2 - secondX1));

		// firstLine & secondLine are parallel -> no interception
		if (den == 0) {
			return null;
		}

		float n1 = ((firstY1 - secondY1) * (secondX2 - secondX1))
				- ((firstX1 - secondX1) * (secondY2 - secondY1));

		float r = n1 / den;

		// -> no interception
		if (r < 0 || r > 1) {
			return null;
		}

		float n2 = ((firstY1 - secondY1) * (firstX2 - firstX1))
				- ((firstX1 - secondX1) * (firstY2 - firstY1));

		float s = n2 / den;

		// -> no interception
		if (s < 0 || s > 1) {
			return null;
		}

		float interX = firstX1 + (r * (firstX2 - firstX1));
		float interY = firstY1 + (r * (firstY2 - firstY1));

		return new Point2D.Double(interX, interY);
	}

}

Ausgabe:

Code:

1
0 -> [99.0, 85.0]
1 -> [80.0, 120.0]
1 -> [88.23529411764706, 134.0]
1 -> [120.0, 134.0]
1 -> [140.0, 100.0]
1 -> [131.42857142857142, 85.0]
4 -> [131.42857142857142, 85.0]
Found intersection at: Point2D.Double[80.0, 120.0]
Found intersection at: Point2D.Double[99.0, 85.0]
Found intersection at: Point2D.Double[88.23529052734375, 134.0]
Found intersection at: Point2D.Double[120.0, 134.0]
Found intersection at: Point2D.Double[140.0, 100.0]
Found intersection at: Point2D.Double[131.42857360839844, 85.0]

Gruß Tom

Thomas Darimont · 21. Juni 2012

Hallo,

hier mal noch ein kleines Interaktives generischeres Beispiel:

Java:

package de.tutorials;
 
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics2D;
import java.awt.Point;
import java.awt.Polygon;
import java.awt.event.MouseEvent;
import java.awt.event.MouseMotionAdapter;
import java.awt.geom.Area;
import java.awt.geom.Line2D;
import java.awt.geom.PathIterator;
import java.awt.geom.Point2D;
import java.awt.image.BufferStrategy;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
import java.util.concurrent.Executors;
import java.util.concurrent.TimeUnit;
 
import javax.swing.JFrame;
 
public class PolygonIntersectionExample extends JFrame {
 
    private BufferStrategy bufferStrategy;
 
    private Area landscapeArea;
 
    private Area intersectionArea;
 
    private Polygon player;
 
    private volatile Point playerPosition;
 
    private List<Point2D> currentIntersectionPoints;
 
    private Runnable processingLoop = new Runnable() {
        public void run() {
 
            landscapeArea = generateArea();
            player = generatePoly(100, 100, 60, 6);
            playerPosition = getLocation();
 
            while (true) {
                Graphics2D g = (Graphics2D) bufferStrategy.getDrawGraphics();
 
                updateState();
                drawScene(g);
 
                g.dispose();
                bufferStrategy.show();
                
                try {
                  TimeUnit.MILLISECONDS.sleep(10);
                } catch (InterruptedException e) {
                  e.printStackTrace();
                }
            }
        }
 
    };
 
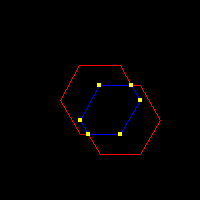
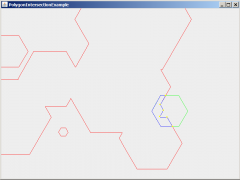
    private void drawScene(Graphics2D g) {
        g.clearRect(0, 0, getWidth(), getHeight());
        g.setColor(Color.RED);
        g.draw(landscapeArea);
 
        g.setColor(Color.GREEN);
        g.draw(player);
 
        g.setColor(Color.BLUE);
        g.draw(intersectionArea);
 
        g.setColor(Color.YELLOW);
        int r = 5;
        for (Point2D point : currentIntersectionPoints) {
            int x = (int) (point.getX() - r / 2.0);
            int y = (int) (point.getY() - r / 2.0);
            g.fillOval(x, y, r, r);
        }
 
    }
 
    protected Area generateArea() {
        Polygon[] polygons = generatePolygons(10, 512, 512, 200, 6, 13);
 
        Area areaUnion = null;
        for (Polygon p : polygons) {
            Area area = new Area(p);
            if (areaUnion == null) {
                areaUnion = area;
            } else {
                areaUnion.add(area);
            }
        }
        return areaUnion;
    }
 
    private void updateState() {
        updatePlayerPosition();
 
        computeIntersectionArea();
 
        List<Line2D> intersectionLines = computeIntersectionLines();
 
        computeIntersectionPoints(intersectionLines);
    }
 
    private void updatePlayerPosition() {
        int x = player.xpoints[0];
        int y = player.ypoints[0];
        player.translate(playerPosition.x - x, playerPosition.y - y);
    }
 
    private void computeIntersectionArea() {
        intersectionArea = new Area();
        intersectionArea.add(landscapeArea);
        intersectionArea.intersect(new Area(player));
    }
 
    private void computeIntersectionPoints(List<Line2D> intersectionLines) {
        // // Schnittpunkte der Geraden ermitteln
        currentIntersectionPoints = new ArrayList<Point2D>();
        for (int i = 0, len = intersectionLines.size(); i < len; i++) {
            for (int j = i + 1; j < len; j++) {
                Line2D firstLine = intersectionLines.get(i);
                Line2D secondLine = intersectionLines.get(j);
                Point2D.Double point = computeIntersectionPoint(firstLine,
                        secondLine);
                if (point != null) {
 
                    // Auskommentieren, falls Punkte innerhalb der Area auch
                    // berücksichtigt werden sollen
                    if (landscapeArea.contains(point)) {
                        continue;
                    }
 
                    currentIntersectionPoints.add(point);
                    // System.out.printf("Found intersection at: %s%n", point);
                }
            }
        }
    }
 
    private List<Line2D> computeIntersectionLines() {
        List<Line2D> intersectionLines = new ArrayList<Line2D>();
        PathIterator pathItr = intersectionArea.getPathIterator(null);
 
        double[] current = new double[2];
        double[] first = null;
        double[] previous = null;
 
        while (!pathItr.isDone()) {
            int coordType = pathItr.currentSegment(current);
            // System.out.println(coordType + " -> " +
            // Arrays.toString(current));
            if (previous != null) {
                intersectionLines.add(new Line2D.Double(current[0], current[1],
                        previous[0], previous[1]));
            } else { // this is the first iteration
                first = current.clone();
            }
            if (coordType == PathIterator.SEG_CLOSE) { // this is the last
                                                        // iteration
                intersectionLines.add(new Line2D.Double(current[0], current[1],
                        first[0], first[1]));
            }
            previous = current.clone();
            pathItr.next();
        }
        return intersectionLines;
    }
 
    public PolygonIntersectionExample() {
        super("PolygonIntersectionExample");
        setDefaultCloseOperation(EXIT_ON_CLOSE);
        this.setPreferredSize(new Dimension(800, 600));
        setupMouseListener();
        setVisible(true);
        createBufferStrategy(2);
        this.bufferStrategy = getBufferStrategy();
        pack();
        startRenderLoop();
    }
 
    private void setupMouseListener() {
        addMouseMotionListener(new MouseMotionAdapter() {
            @Override
            public void mouseMoved(MouseEvent e) {
                playerPosition = e.getPoint();
            }
        });
    }
 
    private void startRenderLoop() {
        Executors.newSingleThreadExecutor().execute(processingLoop);
    }
 
    public static void main(String[] args) throws Exception {
        new PolygonIntersectionExample();
    }
 
    private static Polygon[] generatePolygons(int count, int x, int y,
            int radius, int points, int seed) {
        Polygon[] ps = new Polygon[count];
 
        Random rnd = seed == 0 ? new Random() : new Random(seed);
        for (int i = 0; i < count; i++) {
            ps[i] = generatePoly(rnd.nextInt(x), rnd.nextInt(y),
                    (int) (radius * rnd.nextDouble()), points);
        }
        return ps;
    }
 
    public static Polygon generatePoly(int x, int y, int r, int n) {
        // Quelle:
        // http://www.informatik.htw-dresden.de/~iwe/grundlagen/java/galileo/java_140006.htm#Rxxjava_140006282NEckezeichnen
        Polygon p = new Polygon();
 
        for (int i = 0; i < n; i++) {
            p.addPoint((int) (x + r * Math.cos(i * 2 * Math.PI / n)),
                    (int) (y + r * Math.sin(i * 2 * Math.PI / n)));
        }
 
        return p;
    }
 
    private static Point2D.Double computeIntersectionPoint(Line2D firstLine,
            Line2D secondLine) {
 
        float firstX1 = (float) firstLine.getX1();
        float firstX2 = (float) firstLine.getX2();
 
        float firstY1 = (float) firstLine.getY1();
        float firstY2 = (float) firstLine.getY2();
 
        float secondX1 = (float) secondLine.getX1();
        float secondX2 = (float) secondLine.getX2();
 
        float secondY1 = (float) secondLine.getY1();
        float secondY2 = (float) secondLine.getY2();
 
        float den = ((firstX2 - firstX1) * (secondY2 - secondY1))
                - ((firstY2 - firstY1) * (secondX2 - secondX1));
 
        // firstLine & secondLine are parallel -> no interception
        if (den == 0) {
            return null;
        }
 
        float n1 = ((firstY1 - secondY1) * (secondX2 - secondX1))
                - ((firstX1 - secondX1) * (secondY2 - secondY1));
 
        float r = n1 / den;
 
        // -> no interception
        if (r < 0 || r > 1) {
            return null;
        }
 
        float n2 = ((firstY1 - secondY1) * (firstX2 - firstX1))
                - ((firstX1 - secondX1) * (firstY2 - firstY1));
 
        float s = n2 / den;
 
        // -> no interception
        if (s < 0 || s > 1) {
            return null;
        }
 
        float interX = firstX1 + (r * (firstX2 - firstX1));
        float interY = firstY1 + (r * (firstY2 - firstY1));
 
        return new Point2D.Double(interX, interY);
    }
 
}

Gruß Tom

Polygonverschmelzung

genodeftest

Erfahrenes Mitglied

Thomas Darimont

Erfahrenes Mitglied

genodeftest

Erfahrenes Mitglied

Thomas Darimont

Erfahrenes Mitglied

Anhänge

Thomas Darimont

Erfahrenes Mitglied

Anhänge

Neue Beiträge