MFC openGL,
hab doch geschrieben, dass shortes path eben nicht in NP liegt.
Wollte damit sagen, dass es nicht direkt was mit TSP und Hamilton zu tun hat.

<edit>
Und in wie fern hat eine Änderung von n etwas mit der Komplexität zu tun?
Ein NP Problem wird doch immer exponentiell bleiben... nur dass es bei kleinen n noch ertragbar ist.
</edit>
Saiz hat gesagt.:
Ja das ist ja das problem wie kriege ich den Graphen
Wie dick ist eine Wand? Eine Längeneinheit (wahrscheinlich Pixel) oder kann sie auch dicker sein?
Ich stand auch mal vor dem Problem.
Habe damals von jeder Ecke einer Wand aus eine Linie (horizontal und vertikal) gezogen habe, bis ich auf eine andere (ggf Außen-) Wand gestoßen bin.
Es entstand ein Raster von Sektoren. Das schöne daran war, dass ein Sektor von überall aus mit jedem angrenzenden Sektor erreichbar ist... man kann also einen Sektor auf einen Punkt (normalerweise der Mittelpunkt) reduzieren.
Verbinde die Punkte, die benachbarte Sektoren darstellen und du hast deinen Graphen.
Man kann sich auch von jeder Ecke ein kleines Stückchen diagonal (wenn es die rechte obere Ecke einer Wand ist, dann nach oben rechts) entfernen und da einen Knoten setzen... dann hat man wohl auch wirklich den kürzesten Weg (im ersten Fall würde Dijkstra nicht innerhalb der Sektoren optimieren). Bin mir nur grad nicht ganz darüber im Klaren, wie man dann Nachbarschaft feststelllt.
Saiz hat gesagt.:
WIe kann ich rausfinden das da eine Wand ist?
Keine Ahnung, was zeichnet denn eine Wand aus?
Dass die Pixel da schwarz sind?
Dann vielleicht einfach mal alles abgrasen und dabei benachbarte schwarze Pixel in ein "Wandobjekt" packen.

Dachte, dass du schon Informationen über Wände hast..
/edit2
Oh hab das Beispiel gar nicht gesehen.
Gibt es keine Wände innerhalb des Feldes?
Dann geht es doch vielleicht noch einfacher oder?
Man versucht direkt zum Ziel zu laufen.
Stößt man auf eine Wand, geht man so lange links und rechts an der Wand lang, bis man den Kurs wieder aufnehmen kann.
Bin mir aber nicht sicher, ob es da Probleme geben kann... ist nur eine spontane Überlegung.
/edit3
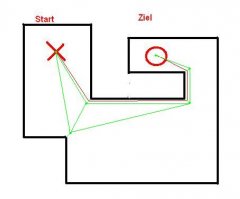
Hab mal den Graphen, den du erzeugen müsstest, in das Beispiel gemalt.
Start und Ziel müssen logischerweise auch noch Konten darstellen.

Wie man da die Nachbarschaft einfach feststellt, weiß ich leider immernoch nicht.
Zur Not einfach jeden Punkt zwischen zwei Knoten (auf direkter Linie) prüfen.
Wie man Wände erkennt... naja, wenn die Zeichnung so ungenau ist, wie in deinem Beispiel, könnte es Probleme geben.

Man braucht ja eigentlich nur die Eckpunkte und Informationen darüber was für eine Ecke es ist (links oben, rechts oben, links unten, rechts unten)...
/edit4
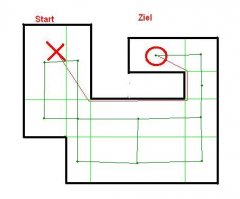
Und hier noch der Graph nach meiner ersten Methode.
Nachteil ist ziemlich eindeutig.
Es werden schnell viele Sektoren (vielleicht auch mal sehr schmale Sektoren).
Ferner wird nicht exakt der kürzeste Weg berechnet und wenn man so wenige große Sektoren hat, wird die Geschichte sehr ungenau.
Dafür hat ein Knoten maximal 4 Nachbarn. Das ist wichtig für Dijkstra, wenn ich mich recht erinnere.
Bei vielen Wänden kann die zweite Methode auch Probleme bereiten, da ein Punkt einer Ecke vielleicht schon hinter oder in einer anderen Wand liegen kann. Das kann bei der ersten Methode nicht passieren.