Matthias Reitinger
ɐɯıǝɹ
Ein Quader ist nicht gerade das einfachste Objekt. Probier es erst mal mit Ebenen und Kugeln. Das reicht zum anfänglichen Herumexperimentieren auf jeden Fall.Hallo
ich versuche mich gerade an einem einfachen RayTracer zu bauen der mit einfachen geometrischen Körpern funktioniert. Und beim einfachstem Objekt , dem Quader bzw Würfel, scheiterts schon.
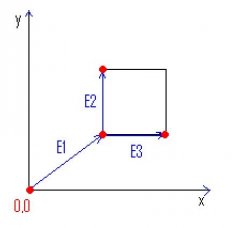
Einfachste Möglichkeit, die mir gerade einfällt: das Rechteck in zwei Dreiecke unterteilen und überprüfen, ob der Schnittpunkt mit der Stützebene in mindestens einem Dreieck liegt (z.B. über baryzentrische Koordinaten).Beim Raytracer verfolgt man ja einen gedachten "Blickstrahl" in die 3D-Scene hinein und behandelt jene Objekte auf die der Strahl trifft. Nun besteht der Körper ja aus 6 Flächen. Mittels Vektorrechnung kann man zwar den Schnittpunkt zwischen Strahl und Ebene berechen, der kann aber außerhalb der Fläche liegen.
Nun zur Frage:
Wie kann ich jetzt berechnen ob der Strahl mit der Fläche kollidiert, um im zweiten Schritt den Schnittpunktberechnung mittels Vektorrechnung zu bestimmen?
Für achsenorientierte Quader gibt es aber noch wesentlich effizientere Algorithmen. Du kannst aber jeden Quader durch eine einfache Drehung an den Achsen ausrichten, also sind solche Algorithmen auch allgemein anwendbar.
Grüße,
Matthias