Programm verrechnet sich beim hochzählen um 0,1

[Tackleberry]

Hallo,
ich habe ein Programm mit einer For-Schleife geschrieben um was zu testen, das mir in einem anderen Programm Probleme bereitet.
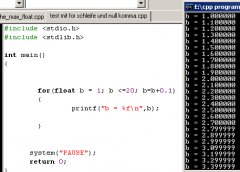
Ich lasse die Schleife laufen bis b <= 20 ist, b startet bei 1. Bei jedem Durchlauf wird b um 0,1 erhöht. Das geht auch bis 2,7 gut. Denn statt 2,8, errechnet das Programm 2,79999 Das ist ziemlich ärgerlich und mathematisch falsch. Woran liegt das?
Den Quelltext und das ausgeführte Programm seht ihr auf dem angehängtem Bild.
Danke.

 

[LordDeath]

Morgen

Ich habs mal probiert ! Mit double statt float "zählt" er richtig.

DarkGreetinx LordDeath

 

[MCIglo]

bis b <= 20 ist,

b ist von Anfang an <= 20. Du meinst eher 'so lange'.

 

[Endurion]

Das liegt daran, dass reale Zahlen (Zahlen mit Nachkommastellen) vom Computer eigentlich nicht darstellbar sind. Teilweise ist das einfach technisch nicht möglich (z.Bsp: Pi hat unendlich viele Stellen).
Da haben sich die Tüftler auf ein paar Konventionen geeinigt, wie man reale Zahlen darstellt. Da ein float nur 4 Byte zur Verfügung hat, gibt es da irgendwo Grenzen, genauso wie bei Ints (32-bit-Compiler, 4 Byte).

Bei floats/doubles gibt es zusätzlich zu einer maximalen und minimalen Grenze auch Genauigkeitsgrenzen. Viele Werte sind einfach nicht direkt darstellbar und deshalb wird da auf den nächst-möglichen Wert ausgewichen. Der Computer "verzählt" sich.

Da double doppelt soviel Speicher belegen darf (8 Byte) ist die Genauigkeit um einiges Besser. Irgendwann wirst du aber auch damit auf Grenzen stossen.

 

[Tackleberry]

Na toll, das heißt, man muss davon ausgehen, das sich das Programm sich immer wieder "verzählen" kann?
Könnte das auch evt. von der CPU abhängen? Als ich meinen Duron übertaktet hatt. Hat das Programm sich schon bei 1,8 "verzählt"...

 

[Endurion]

Sollte eigentlich nicht davon abhängen, aber beim Übertakten können ja sowieso seltsame Dinge passieren.

Wenn du nur einfache Nachkommastellen wie diese hast, bist du vielleicht besser dran, doch mit Ints zu rechnen und an den entsprechenden Stellen zu konvertieren.

(Also statt von 0 mit 0.1 bis 2 von 0 mit 1 auf 20 und an der Stelle, wo der Wert gebraucht wird, mit 0.1f multiplizieren).
Man muss bei real-Zahlen einfach davon ausgehen, dass es keine genauen Werte gibt (also auch nie direkt vergleichen; z.Bsp. if ( fZahl == 3.0f ).
Das klappt dann, wenn fZahl direkt auf 3.0f gesetzt wird, aber zu 99% nicht, wenn da schrittweise hingerechnet wird. Da sollte man dann zum Vergleich das berühmte Epsilon verwenden (if fabsf( fZahl - 3.0f ) < 0.0001f ).