Berechnung der Koordinaten für Beschriftung einer Kuchengrafik

[Marco7757]

Guten Abend

Ich erstelle mit Graphics2D eine Kuchengrafik. Der Kreis ist ganz geschlossen und in mehrere Sektoren eingeteilt. Ich würde nun gerne die einzelnen Teile mit ihrer prozentualen Grösse im Kreis beschriften.
Die Beschriftung soll entweder im Sektor drin, oder ausserhalb der Kreislinie auf der Winkelhalbierenden des Sektor liegen.

Wie kann dies berechnet werden, wenn ich den Radius, die Startkoordinaten sowie die Winkelgrösse habe?

Im Anhang ein Bild, das verdeutlichen soll, an welchen Koordinaten meine Beschriftungen stehen sollen!

Kennt sich jemand mit dieser Art von Mathematik aus und kann helfen?

 

[timestamp]

Gar nicht, dir fehlt noch mindestens eine Zielkoordinate (bzw etwas anderes was die Richtung angiebt).

 

[Marco7757]

Ich weiss ja die Winkel aller Sektoren. Da kann ich doch locker die Winkelhalbierende berechnen. Dann habe ich doch meine Richtung, nicht?

Wenn der Radius beispielsweise 300 Pixel ist, dann wäre die eine Koordinate auf halbem weg (150 Pixel) auf der Winkelhalbierenden, und die andere Koordinate bei etwas mehr als 300 Pixeln, ca. 320 Pixel, ausserhalb des Kreisses auf der Winkelhalbierenden.
Nur ist das Problem, dass ich diese Koordinaten irgendwie noch umberechnen muss, denn (0,0) ist ja nicht in der Kreismitte sondern links oben ...

Hasdt du Ideen oder einen anderen Lösungsvorschlag?

 

[Tomek_FFM]

Beispiel:
Der Mittelpunkt deines Kreises liegt im Punkt (10/10) mit Radius r = 5
Und du hättest einen Winkel Alpha (gerechnet von der x-Achse) von -30°

Dann wären die Koordinaten

- des Punktes a, der auf 2/3 des Radius liegt:
x-Koordinate: 10 + cos(alpha) * 2/3 * 5
y-Koordinate: 10 + sin(alpha) * 2/3 * 5


- des Punktes b, der etwas ausserhalb des Kreises liegt:

x-Koordinate: 10 + cos(alpha) * 6/5 * 5
y-Koordinate: 10 + sin(alpha) * 6/5 * 5


Der Faktor 2/3 bzw. 6/5 schiebt dir den Punkt in den Kreis (wenn der Faktor < 1 ist) oder aus dem Kreis (wenn der Faktor > 1 ist). Dieser ist beliebig anpassbar.

 

[takidoso]

hallole,
habe hier ein Beispiel,welches Dir vielleicht weiterhelfen kann:

import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import java.util.ArrayList;
import java.util.List;

import javax.swing.JPanel;
import javax.swing.SwingUtilities;


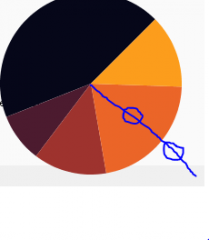
public class PieChartPanel extends JPanel
{
	protected int m_originX;
	protected int m_originY;
    protected int m_radius;
    
  //  final static private  double HALF_PI = Math.PI / 2.0;
  //  final static private  double TWO_PI  = Math.PI * 2.0;
    final static private  double D2R     = Math.PI / 180.0; // Degrees to radians.
    
    private  int    m_xGap  = 5;
    private  int    m_inset = 40;
    
    private  List<Double> m_values = null;
    private  List<String> m_labels = null;
    private  List<Color>  m_colors;
    
	public PieChartPanel()
	{
		createDefaultColors();
	}

	public void createDefaultColors()
	{
		m_colors = new ArrayList<Color>();
		m_colors.add(Color.GREEN);
		m_colors.add(Color.RED);
		m_colors.add(Color.YELLOW);
		m_colors.add(Color.BLUE);
		m_colors.add(Color.PINK);
	}
	
	public void setValues(List<Double> values)
	{
		m_values = values;
	}
	
	public void setLabels(List<String> labels)
	{
		m_labels = labels;
	}
	
	public void setColors(List<Color> colors)
	{
		m_colors = colors;
	}
	
	public void calcPercentagesOfValues()
	{
		double total = 0;
		for (double value : m_values)
		{
			total += value;
		}
		
		for (int i=0; i<m_values.size(); i++)
		{
			m_values.set(i, m_values.get(i)/total);
		}
	}
	
	public void paintComponent(Graphics g)
	{	
		super.paintComponent(g);
		Dimension size = getSize();
		m_originX = size.width / 2;
		m_originY = size.height / 2;
		int diameter = ( m_originX < m_originY ? size.width - m_inset : size.height - m_inset );
		m_radius = ( diameter / 2 ) + 1;
		int cornerX = ( m_originX - ( diameter / 2 ) );
		int cornerY = ( m_originY - ( diameter / 2 ) );
		int startAngle = 0;
		int arcAngle = 0;
		
		
		if (m_values!=null)
		{
			for (int i = 0; i < m_values.size(); i++)
			{
				arcAngle = (int) ( i < m_values.size() - 1 ? Math.round(m_values.get(i) * 360) : 360 - startAngle );
				g.setColor(m_colors.get(i % m_colors.size()));
				g.fillArc(cornerX, cornerY, diameter, diameter, startAngle, arcAngle);
				if (m_labels!=null && m_labels.get(i)!=null)
				{
					g.setColor(Color.BLACK);
					drawLabel(g, m_labels.get(i),  startAngle + ( arcAngle / 2 ));
				}
				startAngle += arcAngle;
			}
		}
		else
		{
			arcAngle = 360;
			g.setColor(Color.LIGHT_GRAY);
			g.fillArc(cornerX, cornerY, diameter, diameter, startAngle, arcAngle);
			g.setColor(Color.BLACK);
			drawLabel(g, "Keine Werte gegeben!",  startAngle + ( arcAngle / 2 ));
		}
		g.setColor(Color.black);
		g.drawOval(cornerX, cornerY, diameter, diameter); // Cap the circle.
		
	}
	
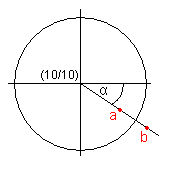
	public void drawLabel(Graphics g, String text, double angle)
	{
		// g.setFont(textFont);
		// g.setColor(textColor);
		double radians = angle * D2R;
		int x = (int) ( ( m_radius + m_xGap ) * Math.cos(radians) );
		int y = (int) ( ( m_radius + m_xGap ) * Math.sin(radians) );
		if (x < 0)
		{
			x -= SwingUtilities.computeStringWidth(g.getFontMetrics(), text);
		}
		if (y < 0)
		{
			y -= g.getFontMetrics().getHeight();
		}
		g.drawString(text, x + m_originX, m_originY - y);
	}
}

habe da vor langer Zeit mal für eine Art Risiko spiel gebraucht, welches ich nie zuende programmiert hatte (mir fehtle die Netzwerk-komponente noch und hatte die Lust verloren)
Anbei ein screenshot von damals mit diesem Diagrammfenster

Viel Spaß damit